1. 문제 설계 배경
최근에 오일러 회로에 대해 공부하게 되었는데, 특정 그래프가 오일러 회로인지를 판별하는 필요충분조건이 매우 간단하다는 점이 인상깊었던 기억이 있다. 이때 특정 그래프가 주어졌을 때 오일러 회로를 구하는 알고리즘도 있지 않을까라는 생각을 했고, 이로부터 오일러 회로를 구해서 풀 수 있는 프로그래밍 문제를 설계해보기로 했다.
2. 문제 설계
제목: 전곽이의 사탕 찾기를 도와줘! (시간 제한: 3초)
문제: 전북과학고에 재학 중인 전곽이는 다른 과학고와 함께 진행하는 미션 계주 대회에 전북과학고 대표로 참가하게 되었다. 이 미션 계주는 N개의 장소가 있는 주어진 코스에서 모든 S개의 길에 각각 하나씩 숨겨져 있는 사탕을 찾고 시작점으로 돌아오는 것이었다. 길을 제대로 찾지 못하여 각각의 길을 여러 번 가며 시간을 낭비하는 것을 막기 위해, 전곽이는 시작점부터 모든 길을 한 번씩만 거쳐서 되돌아올 수 있는 경로를 찾은 뒤에 출발하려고 한다. 전곽이를 위해 경로를 찾아주는 프로그램을 개발하자.
입력: 첫째 줄에 장소의 개수 N(1<=N<=1000)과 길의 개수 S(1<=S<=3000)가 공백으로 구분되어 주어진다. 다음 S개의 줄에는 두 장소를 연결하는 길의 정보가 주어진다. 각 줄은 2개의 정수 u, v로 이루어져 있으며, 이는 장소 u와 장소 v가 길로 연결되어있음을 의미한다.
출력: 출발점을 1이라고 할 때, 전곽이가 갈 수 있는 경로를 거치는 장소 순서대로 공백으로 구분하여 출력하시오. 만약 이 경로가 존재하지 않으면 -1을 출력한다.
입력 예시1
4 4
1 2
2 3
3 4
4 1
출력 예시1
1 2 3 4 1
입력 예시2
6 8
1 2
2 3
3 4
4 1
1 3
3 5
5 6
6 1
출력 예시2
1 6 5 3 1 4 3 2 1
도움말: 미션 계주 경로를 오일러 경로로 생각한다면 쉽게 풀 수 있는 문제이다.
3. 사용한 문제 풀이 전략
사용한 알고리즘: Hierholzer's Algorithm
- 기본 개념 설명
오일러 경로: 모든 간선을 1번씩만 방문하는 연속된 경로
오일러 회로: 시작점과 도착점이 같은 오일러 경로.
오일러 회로의 존재성: 모든 노드의 차수(특정 노드에 연결된 간선의 수)가 짝수면 오일러 회로가 존재한다.
- Hierholzer's Algorithm
본 알고리즘은 오일러 회로를 구하는 데에 가장 효율적이고 널리 알려진 알고리즘이다. 본 알고리즘의 방법은 다음과 같다.
1) 아무 정점 v를 뽑고 v에서 출발하여 v로 돌아오는 경로를 하나 선택한다. (이때 v는 본 문제에서는 무조건 1번 노드가 될 것이다.)
2) 이때, 위 경로에 속해있는 정점 중에서 인접한 간선들 중 경로에 쓰이지 않은 (방문하지 않은 간선이 있는) 정점 u가 존재하면, u에서 시작해 쓰이지 않은 간선들만 사용해 u로 돌아오는 경로를 찾아 원래 경로에 끼워 넣는다.
아래 그래프를 예시로 들어 설명해보겠다.
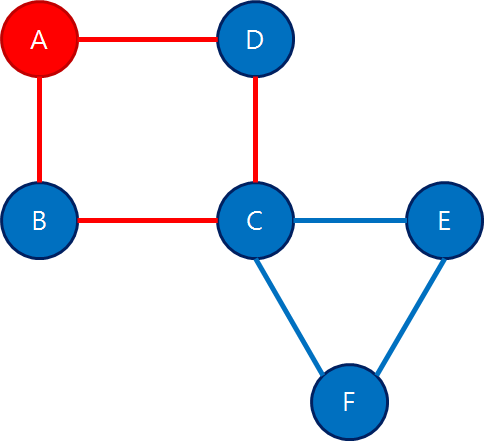
위 그래프의 경우 각각의 노드의 차수가 A는 2, B는 2, C는 4, D는 2, E는 2, F는 2로 모두 짝수이므로 오일러 회로가 존재한다는 것은 쉽게 판단할 수 있다.
위 그래프의 빨간 선처럼 시작점을 A로 놓고 경로 [A, B, C, D, A]를 찾았다고 하자. 그러나 이 중 정점 C는 아직 방문하지 않은 인접한 간선이 존재한다.

따라서 C에서 또다른 경로 [C, E, F, C]를 찾아서 원래의 경로에서 C가 있던 자리에 대체해서 끼워 넣으면 [A, B, C, E, F, C, D, A]가 되어 오일러 회로가 완성된다. 또 만약 경로 [C, E, F, C]의 정점들 중에서 아직 사용하지 않은 인접 간선이 남아있는 정점이 존재한다면 재귀적으로 또 경로를 구해 끼워넣으면 된다.
코드 구현
그렇다면 지금부터 이 Hierholzer's Algorithm을 이용하여 문제를 해결하기 위한 코드를 구현해보겠다.
먼저, 그래프는 인접 리스트 형식으로 표현되어 있다고 하고 오일러 회로를 찾는 함수를 구현해보면 다음과 같다.
def HierholzerAlgorithm(graph):
for node in graph:
if len(graph[node]) % 2 != 0:
return None
stack = [1]
path = []
current_node = 1
while stack:
if graph[current_node]:
stack.append(current_node)
next_node = graph[current_node].pop()
graph[next_node].remove(current_node)
current_node = next_node
else:
path.append(current_node)
current_node = stack.pop()
return path[::-1]위 함수에서는 탐색을 위해 스택을 이용했다. 일단 먼저 오일러 회로가 존재하는지 여부를 파악하기 위해, 각각의 노드의 차수가 모두 짝수인지를 확인한다. 차수가 짝수가 아닌 노드가 있다면 None을 리턴한다.
처음 시작점이 1이므로 초기에는 시작 정점인 1을 넣는다. path는 최종적으로 완성될 오일러 회로를 저장할 리스트이다. current_node는 현재 탐색 중인 정점을 나타내며, 초기에는 1로 설정한다.
이후 스택이 비어있지 않는 동안 현재 정점에 연결된 간선이 존재하면 현재 정점을 스택에 추가한 뒤, 인접 리스트에서 다음으로 이동할 정점을 하나 꺼내고 그 간선을 양방향에서 모두 제거해준다. 그리고 current_node를 next_node로 업데이트해준다. 이때 만약 current_node에 더 이상 연결된 간선이 없다면 현재 정점을 path에 추가한다. 이후 스택에서 바로 직전 정점을 꺼내 current_node로 설정하는데, 이는 지금까지 지나쳐온 정점을 다시 되돌아가며 탐색함을 의미한다. 이렇게 모든 간선을 탐색하면 스택이 비게 될 것이고 결국 오일러 회로를 거꾸로 돈 것이 될 것이다. 따라서 path[::-1]을 통해 리스트를 역순으로 뒤집어 올바른 순서로 반환하면 오일러 회로를 구할 수가 있다.
다음으로는 입력 데이터를 적절하게 처리하여 인접 리스트 형식의 그래프를 만드는 코드를 짜 보겠다.
N, S = map(int, input().split())
graph = {}
for i in range(N):
graph[i+1] = []
for i in range(S):
u,v = map(int, input().split())
graph[u].append(v)
graph[v].append(u)
path = HierholzerAlgorithm(graph)
if path:
for i in path:
print(i,end=' ')
else:
print(-1)이렇게 하면 간선을 입력받으면서 그래프를 인접 리스트로 구현할 수 있고, 앞서 구현한 함수를 이용해 오일러 회로를 출력할 수 있다. 오일러 회로를 가지지 않으면 -1을 출력한다. 실제로 위의 입력 예제 등 다양한 예제를 입력해보아도 올바른 정답을 출력하는 모습을 볼 수 있었다.
전체 코드는 다음과 같다.
def HierholzerAlgorithm(graph):
for node in graph:
if len(graph[node]) % 2 != 0:
return None
stack = [1]
path = []
current_node = 1
while stack:
if graph[current_node]:
stack.append(current_node)
next_node = graph[current_node].pop()
graph[next_node].remove(current_node)
current_node = next_node
else:
path.append(current_node)
current_node = stack.pop()
return path[::-1]
N, S = map(int, input().split())
graph = {}
for i in range(N):
graph[i+1] = []
for i in range(S):
u,v = map(int, input().split())
graph[u].append(v)
graph[v].append(u)
path = HierholzerAlgorithm(graph)
if path:
for i in path:
print(i,end=' ')
else:
print(-1)
4. 시행착오
Hierholzer's Algorithm을 처음 알게 되었는데, 이 알고리즘은 전혀 어렵지 않아서 이해하기에는 무리가 없었다. 그러나 이를 코드로 구현할 때 어려움을 겪었다. 아무 회로를 선택하고 또 경로 사이에 끼워 넣고 이런 것들은 구현하기가 어려웠다. 그래서 이 알고리즘을 코드로 구현하는 여러 방법에 대해 찾아보았고, 결국 본 스택을 이용한 방법으로 구현할 수 있었다.
5. 느낀점
문제를 직접 설계하고 풀어보면서 문제 상황을 자유롭게 설정해보는 과정이 재미있었다. 또한 직접 만든 문제를 풀어보니 뿌듯함도 더 느꼈다. 한편 오일러 회로를 이용한 문제는 처음 풀어 보았는데, 이와 관련하여 해밀턴 회로와 관련된 문제도 관련 알고리즘을 공부하여 풀어보고 싶다는 생각을 하였다.
'AP프로그래밍과 문제해결' 카테고리의 다른 글
| 4. [Python] 객체지향 프로그래밍: One-card game (1) | 2024.06.09 |
|---|---|
| 3. [Python] BOJ 2014 소수의 곱 (1) | 2024.05.01 |
| 2. [Python] BOJ 3015 오아시스 재결합 (2) | 2024.04.01 |
| 1. [Python] BOJ 2243 사탕상자 (2) | 2024.03.17 |


